Le traiettorie dei dischi volanti

Se i dischi volanti viaggiano in linea retta, gli avvistamenti UFO non dovrebbero disporsi lungo corridoi rettilinei?

Da sempre l'uomo vede in cielo oggetti luminosi che non è in grado di riconoscere: le cronache dell'autore latino Giulio Ossequente, vissuto nel IV sec. d.C. riferiscono di avvistamenti di oggetti infiammati dalla forma di lance avvenuti in epoche remote, sin dal 500 a.C. Il suo Libro dei prodigi è una curiosissima raccolta di fatti strani, molti dei quali riferiti proprio a fenomeni celesti che gli antichi non erano in grado di spiegare.

Tale fenomenologia si è riproposta in ogni epoca, ma bisogna aspettare il 24 Giugno 1947 perché nasca ufficialmente quella disciplina che oggi è chiamata "ufologia": quel giorno, un ricco uomo d'affari americano, Kenneth Arnold, racconta di aver visto dal proprio aereo privato almeno 9 oggetti a forma di disco librarsi in formazione nei pressi del monte Rainier, nello stato di Washington. Immediatamente ripreso dalla stampa popolare, questo avvistamento porta all'attenzione dell'opinione pubblica di tutto il mondo il fenomeno degli oggetti volanti non identificati, chiamati UFO dall'acronimo inglese Unidentified Flying Objects. Per diversi anni, le segnalazioni di UFO sono piuttosto sporadiche e sempre caratterizzate da caratteristiche comuni: l'oggetto fa la sua comparsa, viene avvistato e poco dopo sparisce senza lasciare alcuna traccia.

Questa imprevedibilità rende difficile un approccio scientifico alla materia: i primi a voler indagare su questi oggetti sono costretti ad affidarsi alle testimonianze di chi li ha osservati senza mai poter accedere alla "materia prima" delle loro indagini.

Come fa notare con una certa arguzia Charles Harvard Gibbs-Smith, lo studio degli UFO sembra un argomento per gli avvocati molto più che per gli scienziati, perché riguarda le testimonianze di chi vide alcuni oggetti e non gli oggetti stessi.
Il primo a suggerire un metodo per affrontare in modo matematico il fenomeno è un ricercatore francese, Aimé Michel (1919-1992). Siamo nell'autunno del 1954.

❖ Biografia 

Aimé Michel (Saint-Vincent-les-Forts, 1919 – 1992) è stato uno scrittore e filosofo francese specializzato in ufologia. Laureatosi in filosofia, diventa poi insegnante di psicologia e nel 1944 comincia a lavorare alla RDF (Radio Diffusion Française, futura RTF poi ORTF).
Esperto di metodologia, scrittore scientifico, diviene membro del Collège Invisible ufologico di Jacques Vallée negli anni 70. È del 1958 la sua celebre teoria sull'ortotenia secondo cui, su un periodo abbastanza corto di circa 24 ore, gli avvistamenti UFO sono allineati alla faccia della Terra. L'uso di simulazioni al computer ha fatto sì che questa teoria fosse rigettata definitivamente nel 1976. I suoi lettori apprezzano generalmente il suo interesse approfondito per «tutto ciò che oltrepassa l'umano» e le sfide dello spirito.

Qualificato come uno spirito libero dai suoi accoliti ha da sempre avuto come obiettivo il non lasciarsi limitare da nessun contatto esterno.
È stato un grande amico dei controversi Jacques Bergier e Louis Pauwels, autodefinendosi come un «ribelle patologico».

❖ Aimé Michel e l'ortotenia

Nel mese di Settembre 1954 la Francia è teatro di una serie crescente di avvistamenti di oggetti volanti non identificati. Aimé Michel si trova in Costa Azzurra, nella splendida villa del poeta Jean Cocteau a Saint-Jean Cap Ferrat. La conversazione tra i 2 cade sulle recenti segnalazioni che Michel sta pazientemente catalogando. Il poeta ha un'idea:

dovresti vedere se questi oggetti si muovono lungo alcune linee, se stanno tracciando qualche disegno o qualcosa del genere. Potresti cercare di scoprire se i loro movimenti coincidono in modo significativo con le linee magnetiche di forza o con qualche altra linea.

Cocteau è un artista visionario, che riconosce negli UFO un tentativo di mettersi in contatto con noi terrestri;  è naturale per lui cercare di intuirne i messaggi leggendoli nelle traiettorie da loro descritte nel cielo, come se si trattasse di tratti eseguiti con la china su un gigantesco foglio da disegno.

Nonostante la sua mentalità più vicina alla scienza, Aimé Michel si lascia ispirare dalle parole del poeta: inizia quindi a segnare su una mappa della Francia tutte le località presso cui sono segnalati avvistamenti alla ricerca di un "disegno" globale.
Seppure queste siano sparse piuttosto uniformemente su tutto il territorio francese, a tratti emergono delle regolarità che lo impressionano molto: alcuni punti sono allineati tra loro, a suggerire, che i vari avvistamenti seguono la traiettoria di un oggetto che viaggia in linea retta. Il ricercatore capisce che è un momento storico per l'ufologia e  4 anni più tardi, nel suo libro Misteriosi oggetti celesti del '58 scriverà:

dal 17 Settembre 1954 in poi, il fenomeno degli UFO iniziò a perdere quella fatale caratteristica di unicità - fatale perché essenzialmente antiscientifica, costituendo un serio ostacolo per gli studi. Ciò che emerse fu qualcosa che non era più soggetto all'incertezza della testimonianza umana; qualcosa che poteva essere esaminato, studiato ed analizzato attraverso rigorosi metodi scientifici. A questo 《qualcosa》 diedi il nome provvisorio di ortotenia.

Il termine deriva dall'aggettivo greco orthoteneis, che significa "disposto su una linea retta".

Nell'ambito degli UFO, una serie di avvistamenti che si disponessero lungo una retta potrebbero suggerire l'esistenza di qualche stimolo visivo che si manifesta su una traiettoria lineare.

Con l'introduzione di questa ipotesi, l'ufologia si dotava della possibilità di esaminare matematicamente i punti disposti su una mappa per valutare se gli allineamenti rilevati fossero dovuti al caso, o, se invece, suggerissero l'esistenza di "qualcosa" che viaggia linearmente e che quindi viene avvistato lungo "corridoi" privilegiati.

❖ Come studiare gli allineamenti

Trovare qualche allineamento non basta: anche scegliendo a caso alcuni punti, questi potrebbero disporsi lungo linee rette. Dobbiamo quindi confrontare gli allineamenti riscontrati con quelli che si verificherebbero su una mappa popolata casualmente; in altre parole, dobbiamo fare i conti con la "mappa media" (che chiameremo Mediomap), la mappa i cui punti sono distribuiti in modo del tutto casuale.

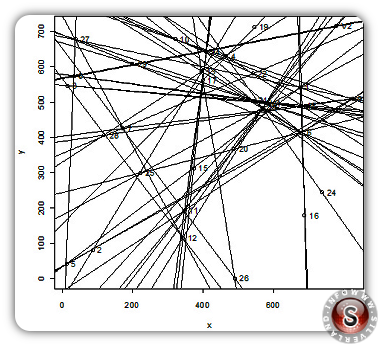
È Alexander D. Mebane il primo a proporre un confronto del genere, utilizzando una mappa della costa orientale degli Stati Uniti su cui ha riportato 27 avvistamenti avvenuti il 6 Novembre 1957. I computer non sono ancora accessibili al grande pubblico e quindi l'esperimento da lui suggerito è piuttosto artigianale, ma non meno efficace:

chiunque abbia tempo e pazienza sufficienti, può provare a contare le linee pseudo-ortoteniche che si presentano in un gruppo di punti scelti casualmente. Per farlo, sparpagliate su un foglio di carta piatto dei piccoli semi alla rinfusa.

Si tratta del modo più veloce per realizzare una mappa casuale.

Una volta fissati tali punti, bisogna tenerne traccia con un pennarello e collegarli due alla volta con un righello, verificando se i segmenti così tracciati incrociano altri punti.

Alla fine si contano gli allineamenti ottenuti casualmente in questo modo, tenendo nota di quanti siano gli allineamenti di 3 punti 4 punti, 5 punti, eccetera.
Il procedimento va ripetuto più volte, per poter fare la media dei risultati ottenuti nel corso dei vari tentativi, arrivando così a definire quanti allineamenti si presentino casualmente sulla mappa media. Attraverso questo lungo e complicato procedimento, da lui effettuato con semi di erba gatta, Mebane mette a confronto gli allineamenti della mappa statunitense e quelli della Mediomap, ottenendo questi risultati:

                                                                            2 P*            3 P*          4 P*          5 P*
27 avvistamenti del 6 Novembre  '57          278               17              2                1
27 punti casuali Mediomap                          252                25             4                 0
 
Un semplice test statistico rivela che non esistono "allineamenti privilegiati" tra gli avvistamenti americani del 6 Novembre 1957, perché è minima la differenza tra i risultati ottenuti sulla mappa e quelli ottenuti sulla Mediomap.

P* = PUNTI

Nel 1966 Janine e Jacques Vallee pubblicano L'enigma UFO, una sfida alla scienza, un interessante studio scientifico sugli oggetti volanti non identificati: il loro approccio alla materia è rigoroso e, ampio spazio viene dedicato all'ortotenia.

Sull'argomento hanno una posizione di grande equilibrio, ammettendo, che le osservazioni di Michel sono corrette, ma anche che:

"bisogna studiare con attenzione l'idea dell'ortotenia, specie il ruolo giocato dal caso nel realizzare le strutture lineari".

Con grande pazienza, i 2 autori registrano in un primo rudimentale database tutti gli avvistamenti di cui hanno notizia, in particolare, quelli relativi al "caldo" autunno del 1954.
Memorizzati in un computer, i punti vengono catalogati a seconda del grado di attendibilità della segnalazione e della data in cui è stato fatto l'avvistamento, in modo da poterli studiare suddivisi in giornate. A questo punto, entra in gioco l'analisi matematica.

Se prendiamo una manciata di punti tra tutte le possibili linee rette, ce n'è una che è la più "vicina" ai punti stessi: si chiama "retta di regressione".

Calcolarla a mano è lungo e complicato, ma con un moderno calcolatore è questione di poche frazioni di secondo. A questo punto, calcolando la distanza dei vari punti da questa retta, possiamo dire che sono tutti "allineati" se tali distanze sono sempre inferiori ad un valore predefinito. Ecco un esempio pratico:

consideriamo 4 città dove potrebbero essere state avvisate strane luci nel cielo: Torino, Milano, Pavia e Venezia.

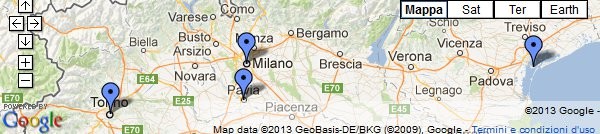
Chiedendo al computer di calcolare la retta di regressione, si ottiene questo:

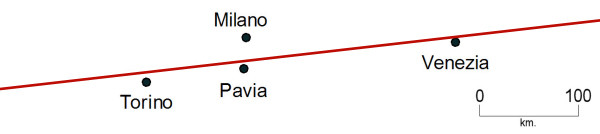
Se calcoliamo la distanza in Km di ogni città da questa linea, otteniamo questi valori:

• 10 km Torino
• 23 km Milano
• 09 km Pavia
• 05 km Venezia

Le città sono allineate o meno?

Dipende da quanto siamo severi. Se concediamo alle città di trovarsi ad una distanza massima dalla linea di 25 km, allora possiamo considerarle in qualche modo "allineate".

Se però siamo più severi e concediamo soltanto una distanza massima di 10 km, vediamo subito che Milano è fuori dal limite consentito; per questo motivo, le 4 città si dicono "complessivamente non allineate". Fissiamo un limite rigido: accettiamo qualsiasi allineamento tale per cui le città non siano più distanti di 1 km dalla retta di regressione.

Poiché per parlare di allineamento si devono avere almeno 3 città, il computer passa in rassegna tutte le possibili triplette, ognuna con la sua retta e per ognuna verifica se le città si trovano tutte entro un Km da essa. Durante l'analisi della tripletta costituita da Torino, Pavia e Venezia, il computer calcola questa retta di regressione:

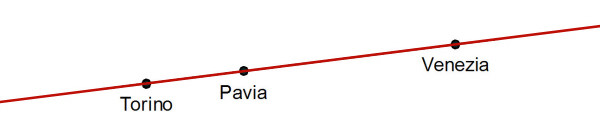
Le 3 città si trovano tutte entro un Km dalla linea, quindi, si possono dire "allineate".

Proseguendo nella scansione, il computer si trova ad esaminare la tripletta di Torino, Milano e Venezia, la cui retta di regressione è questa:

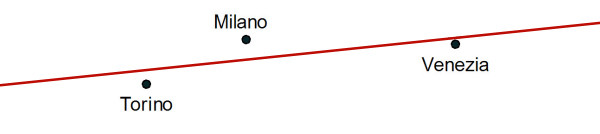
La linea è però troppo distante dai 3 centri abitati:

Milano è distante più di 20 km da essa e quindi, le 3 città sono giudicate "non allineate".
Dopo aver esaminato tutte le triplette, il computer passa ai gruppi di 4 città e così via, fino a verificare tutte le possibili aggregazioni dei punti in gioco.
Nel caso delle 4 città su considerate, le verifiche necessarie sono soltanto 5 e, l'unico allineamento degno di interesse è di 3 punti: quello che lega Torino, Pavia e Venezia:

3 punti › Torino, Milano, Venezia › Non allineate
3 punti › Torino, Pavia, Venezia › Allineate
3 punti › Torino, Milano, Pavia › Non allineate
3 punti › Milano, Pavia, Venezia › Non allineate
4 punti › Torino, Milano, Pavia, Venezia › Non allineate

I moderni calcolatori consentono non soltanto di analizzare le mappe di avvistamenti, ma, anche di elaborare le mappe casuali in modo del tutto virtuale evitando di sparpagliare semi di erba gatta sulla scrivania. Poiché abbiamo definito con precisione che cosa sia un allineamento, occupiamoci di un caso reale che Aimé Michel considerò tra i più notevoli di quell'autunno 1954: i 31 avvistamenti registrati in Francia il 2 Ottobre 1954.

❖ Gli UFO del 2 Ottobre 1954

Sul suo libro Misteriosi oggetti celesti Aimé Michel pubblicò questa mappa, mettendo in rilievo in particolare l'allineamento di 6 punti lungo la direttrice Les Rousses, Dijon, Poncey, Provins, Voinsles e Maisoncelles-en-Brie.

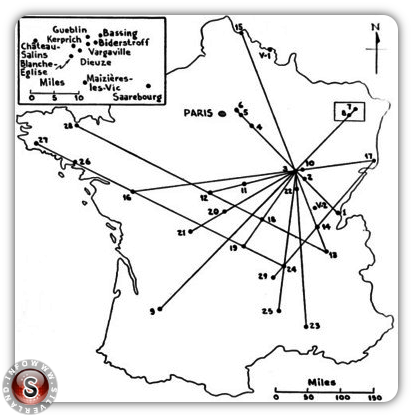
Dobbiamo ora trasferire i punti dalla mappa al piano cartesiano:

ogni avvistamento corrisponderà ad un punto, ed ogni punto sarà individuato dalle 2 coordinate x e y (espresse in Km). Ecco il piano corrispondente:

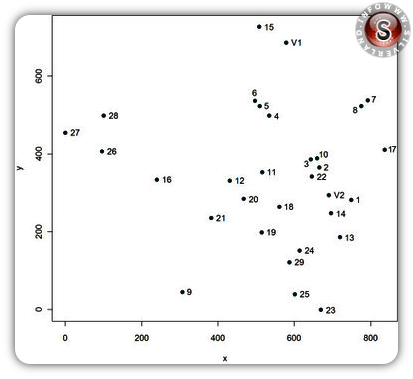
Il computer conta in pochi secondi tutti gli allineamenti entro un margine di tolleranza di 2 km, ottenendo questo risultato:

                                                                               2 P*       3 P*       4 P*       5 P*      6 P*
31 avvistamenti del 2 Novembre '54              149         59          19            1           1

Come si può vedere, il calcolatore si accorge dell'allineamento a 6 punti segnalato sulla mappa da Aimé Michel. Con lo stesso programma è possibile calcolare gli allineamenti di una mappa media casuale delle stesse dimensioni di quella utilizzata dal ricercatore francese; il loro numero medio, arrotondato all'unità è il seguente:

                                                                               2 P*        3 P*       4 P*       5 P*       6 P*
31 punti casuali Mediomap                              304           47          3             0             0

Se si effettua un test statistico per confrontare le 2 mappe, risulta che la mappa di Aimé Michel presenta un numero maggiore di allineamenti rispetto a quelli che ci si aspetterebbe dal caso; in parole semplici, gli avvistamenti si dispongono lungo corridoi molto più di quanto farebbero dei semi buttati a caso su un foglio di carta.

È la prova che i dischi volanti viaggiano in linea retta?

P* = punti

❖ L'ortotenia e il trucco della selezione

L'analisi di Aimé Michel presentava diversi problemi e lui stesso era piuttosto cauto nel proporre le sue mappe con gli allineamenti. Il ricercatore spiegava, ad esempio, che bisogna considerare che la Terra è sferica e che quindi una linea "retta" dal punto di vista teorico è in realtà una curva che segue la superficie terrestre e descrive una circonferenza intorno al globo; studiare i punti su una mappa piatta, come quelle che abbiamo comunemente a disposizione, richiederebbe di tenere conto di questa distorsione.

Inoltre, alcuni degli avvistamenti che si dispongono in linea retta potrebbero riferirsi ad aerei di linea, meteoriti o satelliti che non vengono riconosciuti come tali: scoprire che esistono allineamenti significativi dimostrerebbe soltanto che lo stimolo all'origine degli avvistamenti viaggia in modo lineare, ma, non ci direbbe nulla sulla natura dell'oggetto stesso.
Ma c'è un secondo problema di cui Michel non parla del quale però abbiamo qualche indizio.

Se tornate alla mappa da lui proposta, vedrete che 2 punti non seguono la normale numerazione, ma si chiamano V1 e V2. Il ricercatore li ha battezzati "dischi virgiliani", dal nome del poeta latino Virgilio, che nell'Eneide (raccontando di un tremendo naufragio) parla di rari nantes in gurgite vasto, riferendosi a quei pochi nuotatori che compaiono sparsi qua e là tra le acque: si tratta di avvistamenti che non sembrano disporsi lungo alcun allineamento e che quindi si ribellano a qualsiasi schema ortotenico, comparendo appunto "qua e là" sulle mappe in modo irregolare. Dei 31 avvistamenti indicati sulla mappa, soltanto 2 sono da lui considerati "virgiliani", ma quanti altri avvistamenti avvennero quel giorno e non furono inclusi in questa lista? I 29 punti considerati sono forse una selezione di tutte le segnalazioni ricevute il 2 Ottobre 1954?

È Donald Menzel ad avanzare tale ipotesi in una lettera alla rivista inglese Flying Saucer Review, dove scrive:

"Michel fa riferimento a oltre 600 avvistamenti francesi. […]

Eppure ne considera solo alcuni nelle sue analisi statistiche e non spiega perché ha selezionato alcuni avvistamenti e ne ha ignorati altri. […]

I dati vengono suddivisi per date di calendario. Questo significa che un avvistamento dopo la mezzanotte dovrebbe essere attribuito al giorno successivo. […]

Ma il 24 Settembre alle 3 di notte un avvistamento a Vierzon si trova vicino ad una linea definita il giorno prima e quindi Michel lo registra come avvenuto il 23-24 Settembre e lo traccia sulla mappa del 23 Settembre. […]

A volte aggiunge un avvistamento avvenuto a Roma o in Africa, soltanto se si allinea ad una traccia preesistente; chiaramente lo ignora se non si allinea".

Esiste anche il problema inverso, ovvero, la possibilità che ulteriori avvistamenti vengano esplicitamente cercati per completare linee altrimenti "scarse"; è sempre Menzel a segnalarlo:

"supponiamo che si individui su una qualche mappa un allineamento di 4 punti.

(L'ufologo) potrebbe voler trovare altri avvistamenti che confermino la realtà di questa linea.

E' semplice farlo, scrivendo a qualche amico, al giornale locale o al postino di diverse città, chiedendo notizia di eventuali avvistamenti in una certa data.

Si può star certi che almeno 2 risposte arriveranno: l'allineamento a 4 punti diventerà di 6 punti".

In un suo articolo del 1963, Aimé Michel commise l'ingenuità di ammettere l'errore imputatogli da Menzel; a proposito della linea più famosa da lui identificata, la BAVIC, che attraversa Bayonne e Vichy, scrisse:

"era necessario organizzare un monitoraggio sistematico delle regioni attraversate dalla linea BAVIC. E questo è stato fatto qui in Francia sin dall'autunno 1962".

Se l'area attraversata da una linea viene monitorata con più attenzione rispetto alle regioni confinanti è ovvio aspettarsi un maggior numero di avvistamenti in quella zona, ma non a causa dell'ortotenia, quanto del fatto che è all'opera il tipico trucco statistico della "selezione". L'approfondita analisi che Janine e Jacques Vallee fecero delle mappe di Aimé Michel, prese il via da una verifica sistematica di ogni punto considerato.

Ciò mise in luce un altro problema che poteva gravemente inficiare i risultati ottenuti: alcuni resoconti di avvistamenti infatti provenivano da articoli di giornale che non riportavano il luogo esatto dove era avvenuto, bensì, la città di residenza del testimone; se il punto veniva collocato su quest'ultima, la mappa risultante era chiaramente erronea e qualsiasi analisi ne era gravemente inficiata. Altri avvistamenti dovevano essere esclusi dall'analisi perché effettuati da aerei in volo; in questo caso, era impossibile la registrazione del punto preciso dove l'oggetto era stato rilevato. Verificando il database dei Vallee, viene in luce il fatto che diverse delle 6 città lungo il "corridoio" rilevato il 2 Ottobre 1954 (tra cui Les Rousses, Poncey e Provins) presentavano alcuni di questi problemi: in effetti, tale linea resterà un caso isolato, successivi avvistamenti non daranno conferme della sua esistenza e verrà presto abbandonata. Il tema tornerà più volte al centro dell'attenzione degli ufologi, ma, senza risultati di rilievo: perfino il più importante rapporto mai compilato sull'argomento, il Condon Report del 1968, si esprimerà in modo piuttosto critico nei confronti dell'ipotesi ortotenica e, lo stesso Michel, arriverà ad ammettere tutti i limiti della pista da lui suggerita.

Fonte